-
Earth Science Journal!
#8
Title: Minutes of Distance!
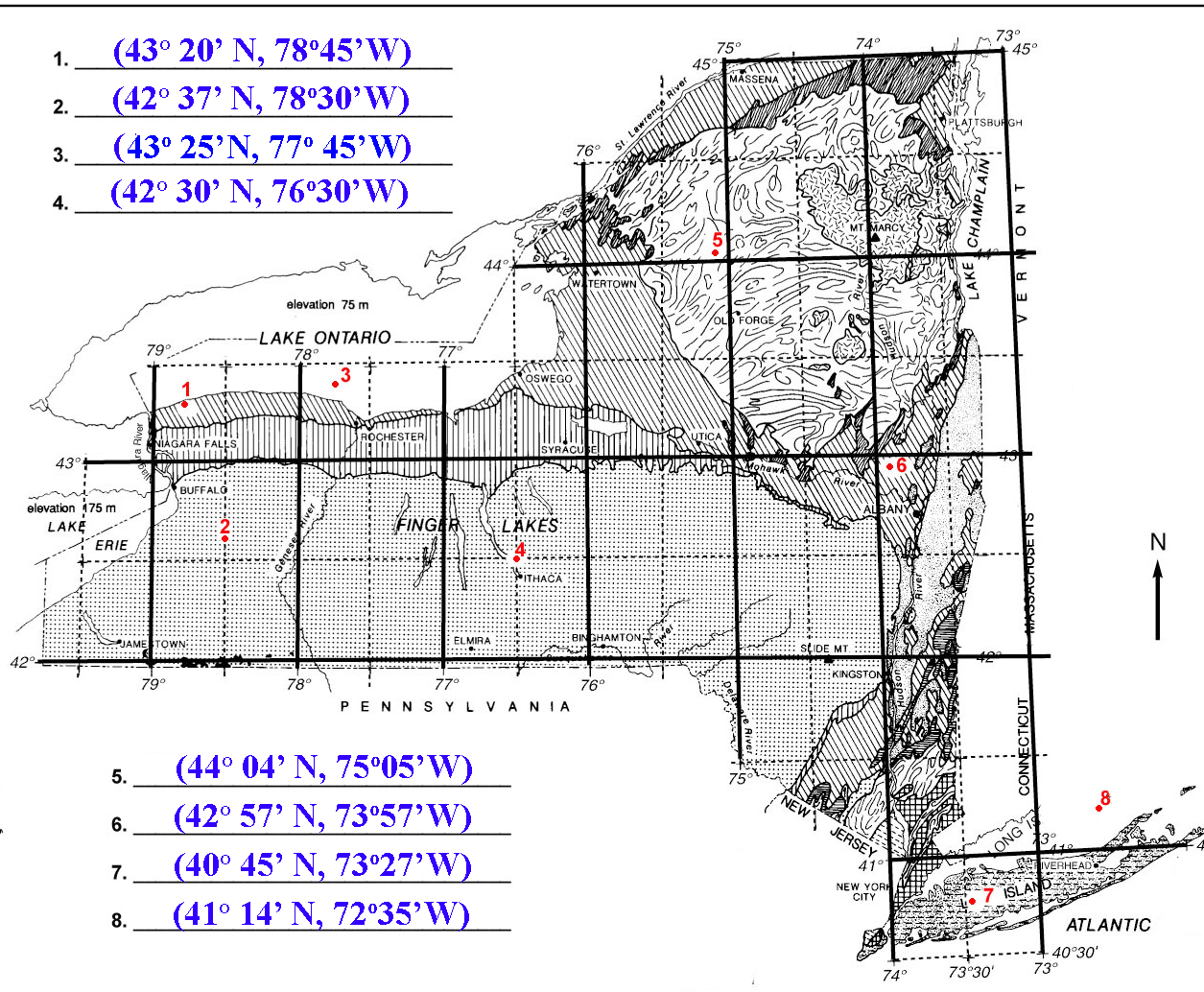
Draw this set of squares about 8 cm by 8 cm.
Plot the above latitude and longitude and mark it with a dot.
Take your best guess.
Journal Notes
Degrees of Latitude and Longitude are divided up into smaller units called minutes. Similar to how an hour of time has 60 minutes, each degree of Latitude or Longitude also has 60 minutes (60').But these are minutes of distance!
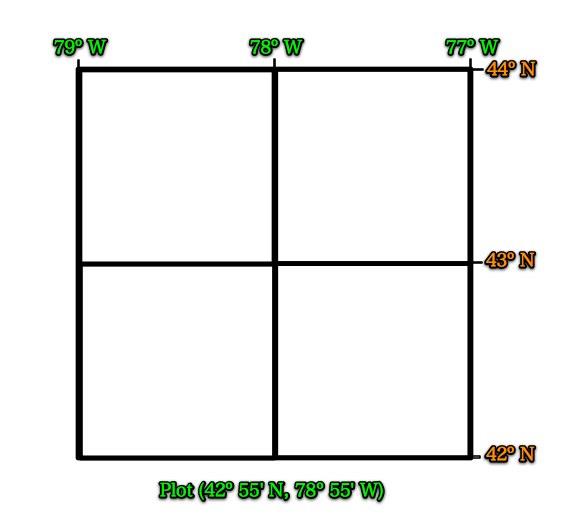
If we divide one degree of latitude into half, we have the 30' mark.
In this case, that line is 42° 30' North Latitude.
Draw and label this line.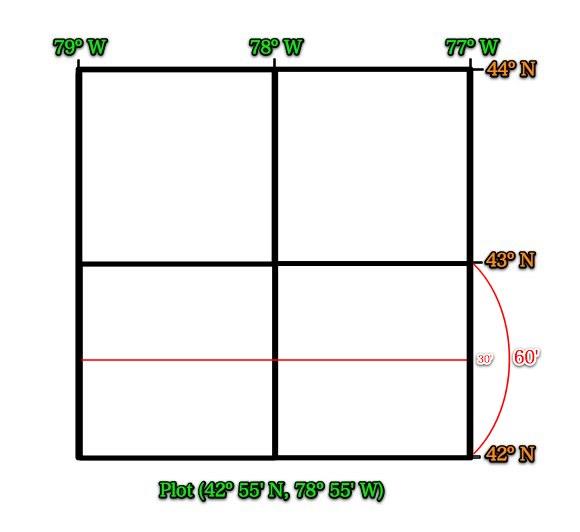
We can then divide further to plot more precisely.
What are the values of these lines?
Label them.
Where is the 42° 55' North line of Latitude?
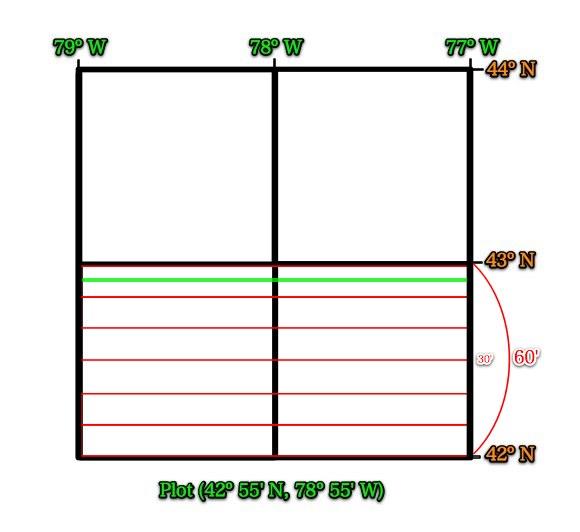
42° 55' North is the green line above.
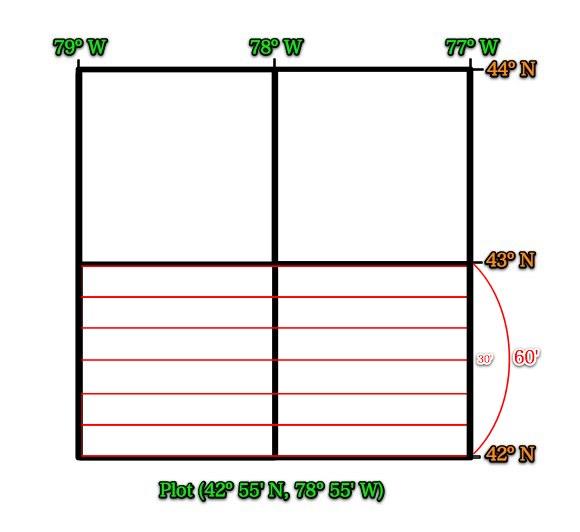
Now, do the same with longitude.
We can divide it up differently and still get a good estimate.
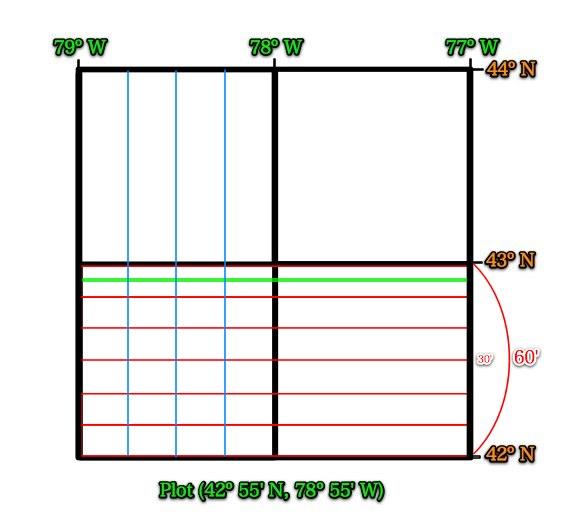
What are the values of the blue lines?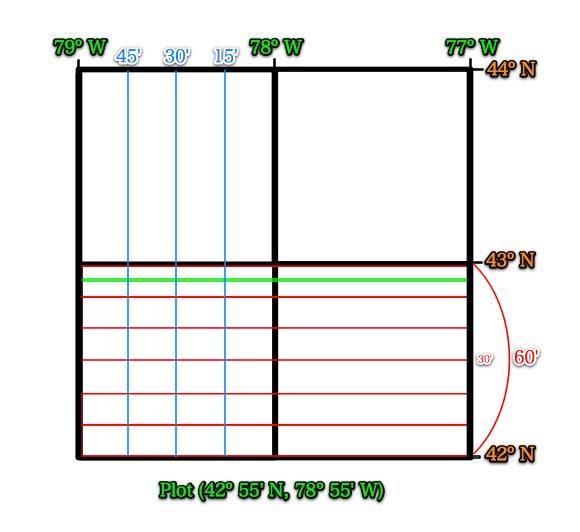
Now try to re-plot the above coordinates and mark it with a dot.
Did you get the dot correct?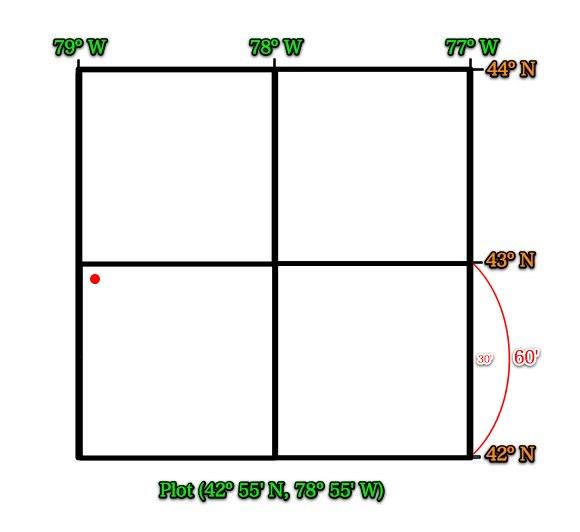
Please take out your reference tables and a ruler.Drawing lines of latitude!
Drawing lines of longitude!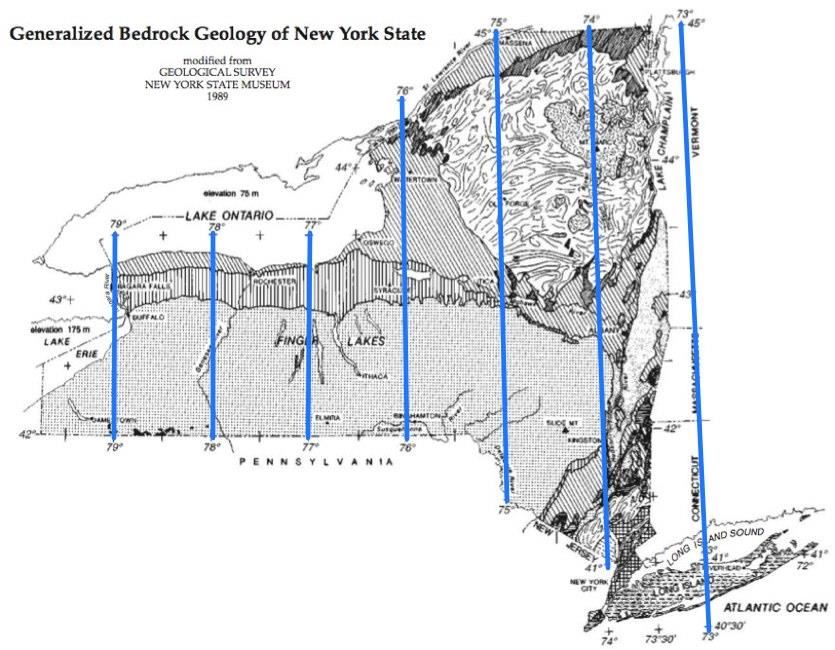
What do you notice about these "straight" lines?The lines are closer together toward the north.
Remember: Longitude lines all meet at the Poles.
Now draw the 30` lines of longitude.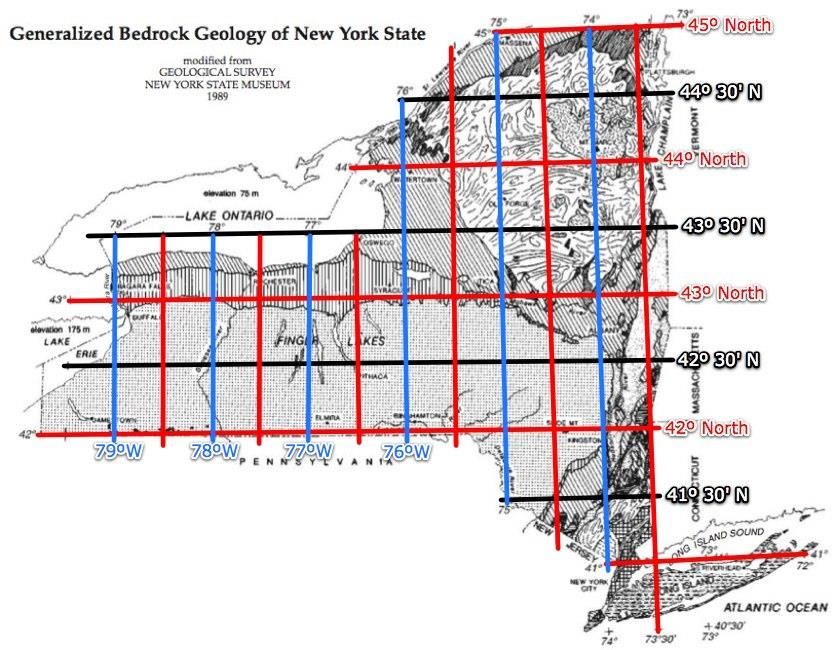
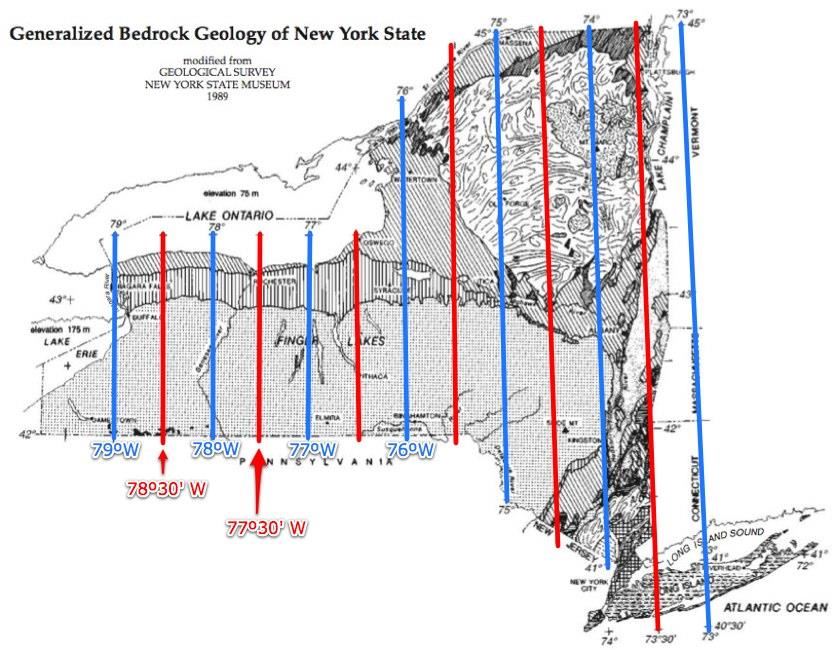
Label a few of these 30' lines.
Use this map to find the city closest to your plotted dot.
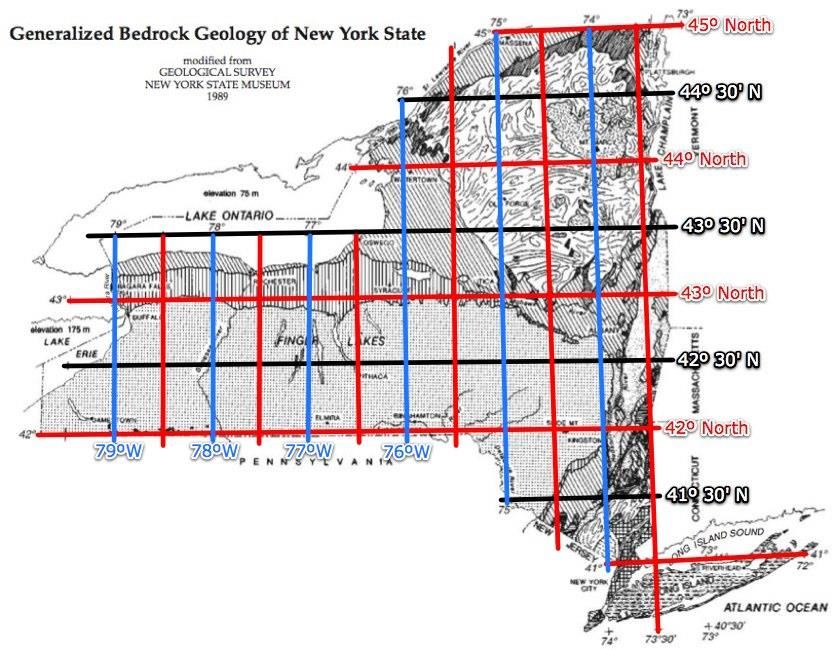
Use this map to find the city that is closest to your coordinates.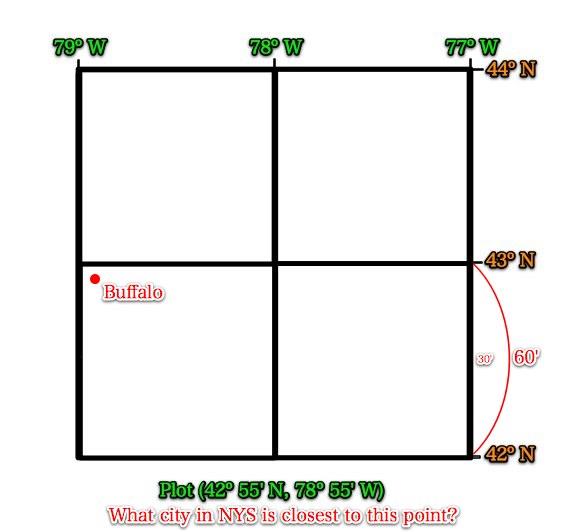
Did you find your answer to be Buffalo?
If so, you are absolutely correct!
Example #2
Draw the following in your journal.
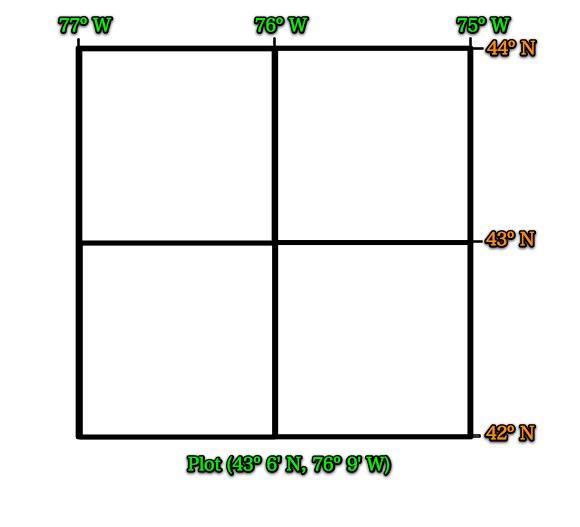
Plot the above latitude and longitude and mark it with a dot.
Find the city in NYS that is located closest to this location.
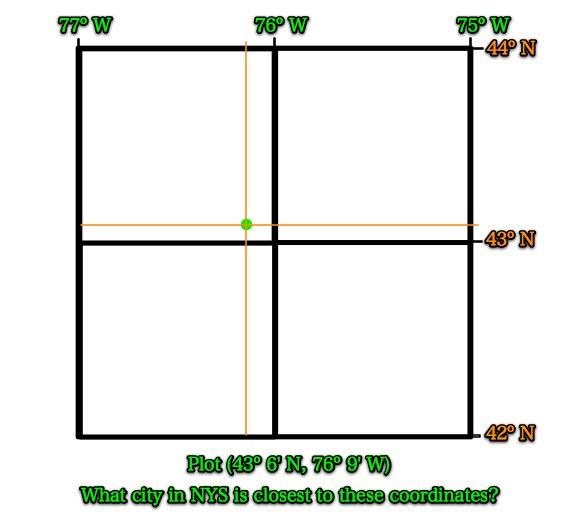
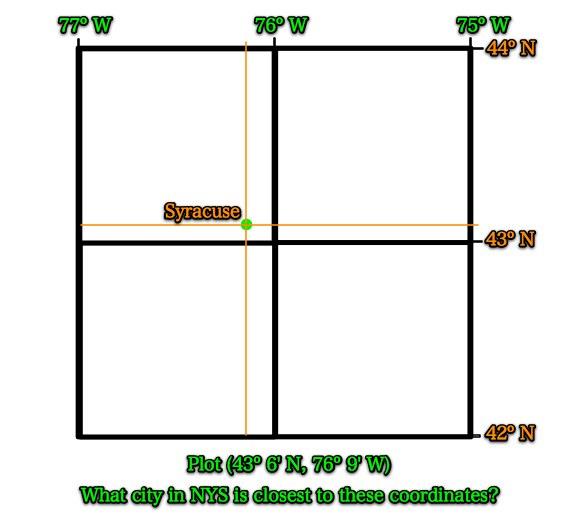
Please write down and answer these questions in your journal.
1. What geologic period is the bedrock in Syracuse, NY? (page 3)
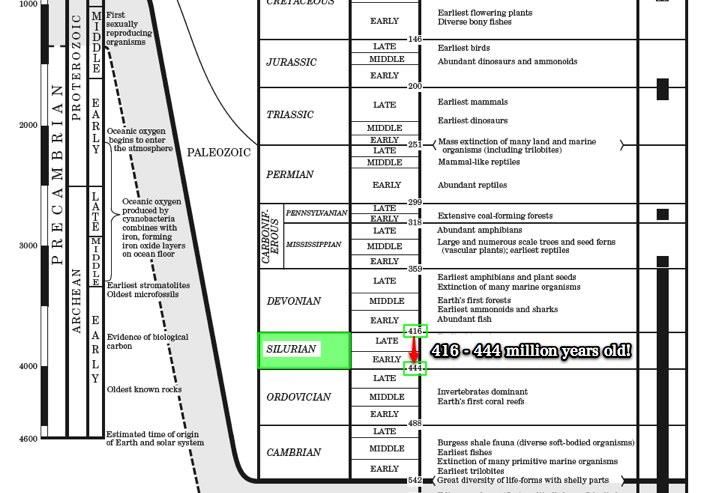
2. How old (in millions of years) is the bedrock in Syracuse, NY? (pages 8 + 9)
3. What is the Landscape Region in Syracuse, NY? (pages 2 and 3)
4. Is our bedrock older or younger than that of Syracuse? (pages 3 and 8)
5. Would we be able to find an Eurypterus in our bedrock?
Why or why not? (pages 3 and 8 + 9)
Answers
1. What geologic period is the bedrock in Syracuse, NY?
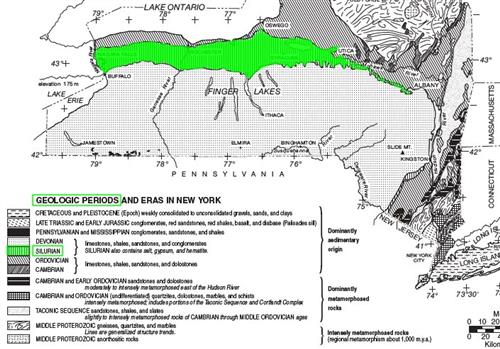
Syracuse's bedrock is from the Silurian Period.
This key shows the youngest bedrock at the top of the key.
2. How old (in millions of years) is the bedrock in Syracuse, NY?
3. What is the Landscape Region in Syracuse, NY?
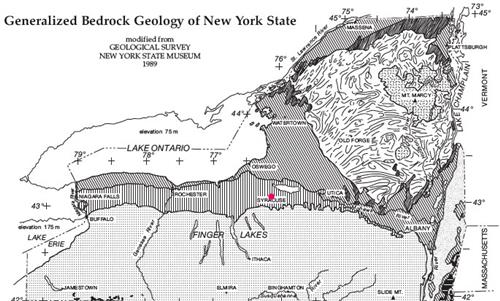
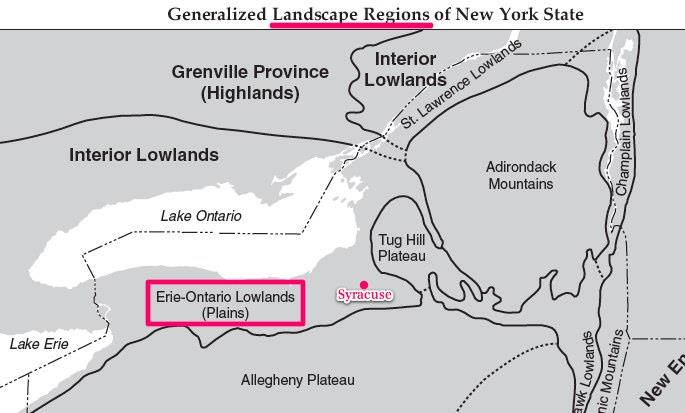
Syracuse is located within the Erie Ontario Lowlands, just like us here in Wilson.
4. Is our bedrock older or younger than Syracuse?
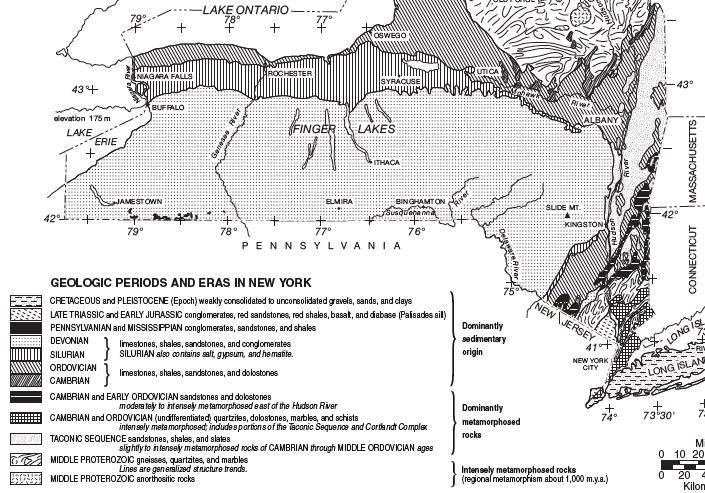
Our bedrock is from the Ordovician Period, which occurred 488 - 444 million years ago.
This is older than the Silurian.
5. Would we be able to find a Eurypterus in our bedrock? Why or why not?
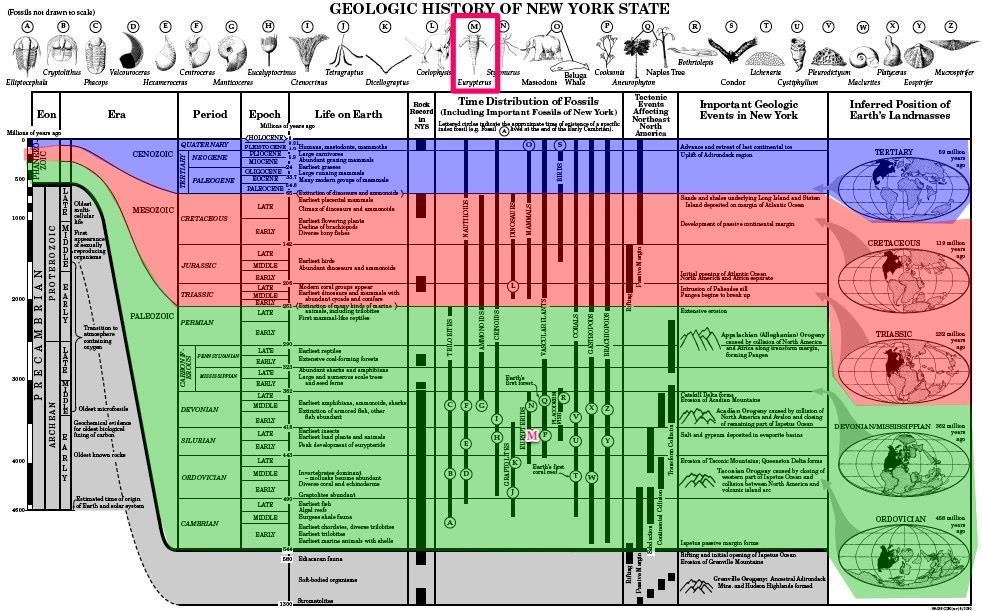
The center of the lettered circle was when the index fossil lived.
Eurypterids are only found in the Silurian Period about 425 million years ago. Our bedrock is too old, for it originated during the Ordovician Period between 443 and 490 million years ago.
Life in the Silurian sea!
http://langsfossils.com/index.php/fossils-for-sale
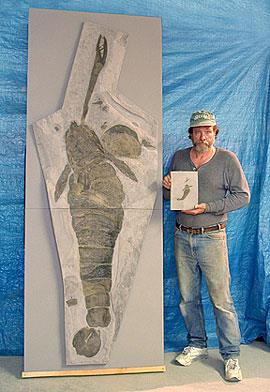
Some of these eurypterids could become huge!
How much are some of these fossils worth?
Fossil hunters make bucks!
Reflection
How do you plot latitude and longitude to the nearest minute?
How were latitude and longitude used to answer other questions in your reference tables?
Bonus!
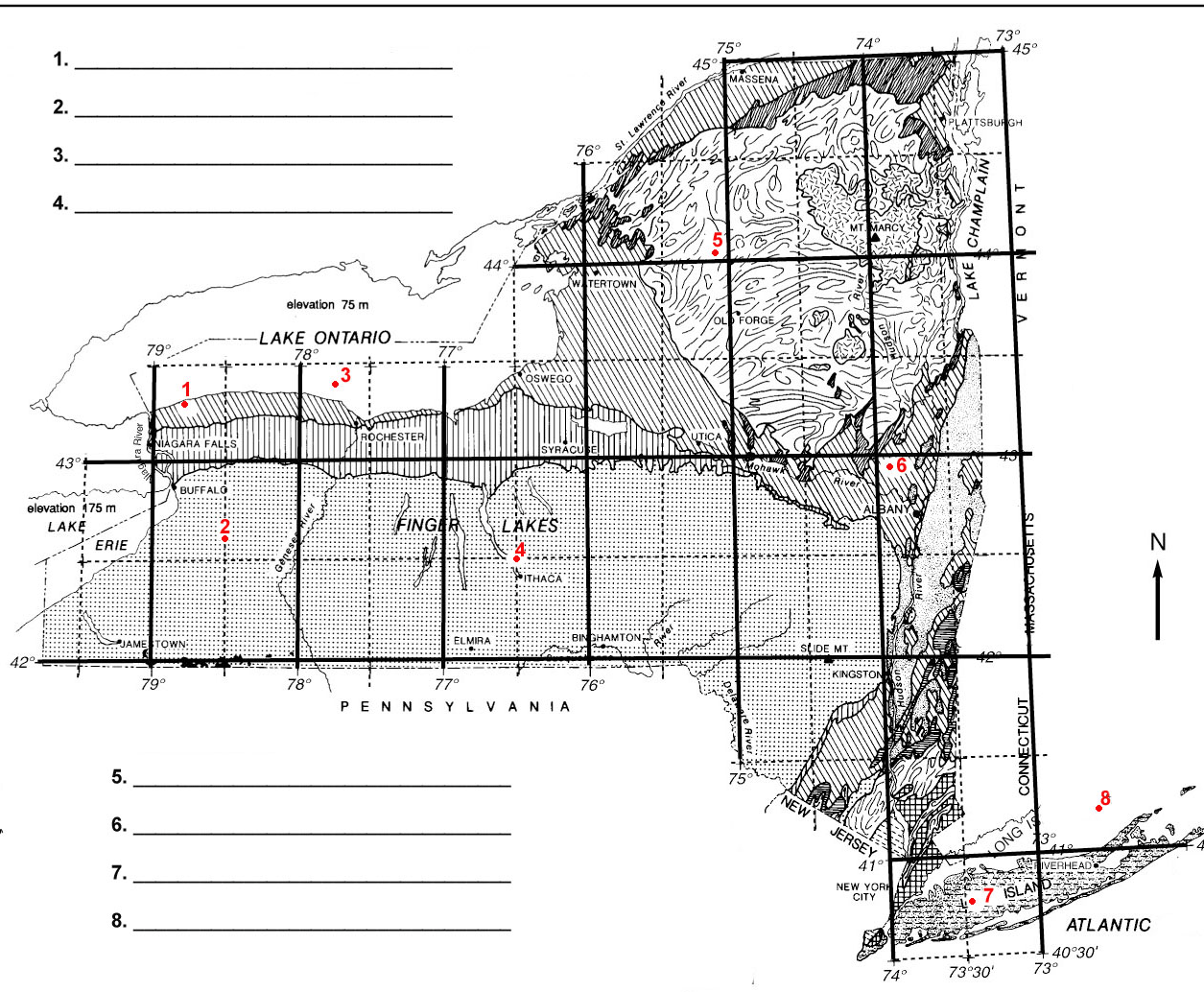
Find the latitude and longitude for the following points to the nearest minute of a degree.
Print out this article and answer the questions in your journal.
Why 360 degrees? 60 minutes? 60 seconds?
http://astro.unl.edu/naap/motion1/tc_history.htmlThe ancient Sumerians (some 4000 years ago) used a base 12 system instead of base 10 like we do today. This seems somewhat natural as 12 is the number of finger segments (three for each finger) that one can count with one's thumb (4 fingers × 3 segments = 12). It takes the moon to go through one full cycle of lunar phases in about 29.5 days, which is why a month has about 30 days (one Moonth). If you take the 365 days in one year and divide it by 29.5, you get about 12 months/year. And so, the year was split into 12 segments. So our calendar year is based upon Earth's and moon's motions, as they revolve around the Sun. One spin of the Earth = one day, one orbit (revolution) of the moon around the Earth = one month, and one revolution of the Earth + Moon around the Sun = one year. It is interesting that our 360-degree circle division has its ancient origins in the largest circle imagined at the time, none but the path of the Earth circling the Sun.
The ancient Babylonians inherited this Sumerian twelve concept and marked the passage of the year with 12 constellations of the Zodiac. They also used a base 60 system and divided a circle into 360 degrees (the ancient Egyptians, who heavily influenced the Babylonians, also had a 360-day year). Being based on 60, each degree could be subdivided into 60 subsegments (minutes), and those 60 subsegments further subdivided into 60 (seconds), and so on. This method, in concept, is essentially identical to our modern method of base 10 decimals.
The ancient Babylonians were excellent mathematicians and astronomers (and mathematics and astronomy were intimately tied back then). Their influence permeated the ancient world and still has a prominent effect today. Thus, today you are still taught about 360 degrees in a circle. And our coordinate system (latitude, longitude), which was tied to astronomical observations originally, uses the minute and second notation. The only difference today is that instead of subdividing seconds into sixtieths (as was done historically), we use the base 10 decimal notation to subdivide seconds.
Answer these questions in your journal.
1. How did we come to have 12 months in one year?
2. How many degrees/day does the Earth travel in orbit?
Show your work.
